Our Submission “A Massively Parallel Algorithm for the Approximate Calculation of Inverse p-th Roots of Large Sparse Matrices” has been accepted for publication at the Platform for Advanced Scientific Computing (PASC) conference, taking place in July 2018 in Basel, Switzerland. The paper is the result of combined effort by members of the Departments of Computer Science and Chemistry at Paderborn University, the Paderborn Center for Parallel Computing and the Barcelona Supercomputing Center.
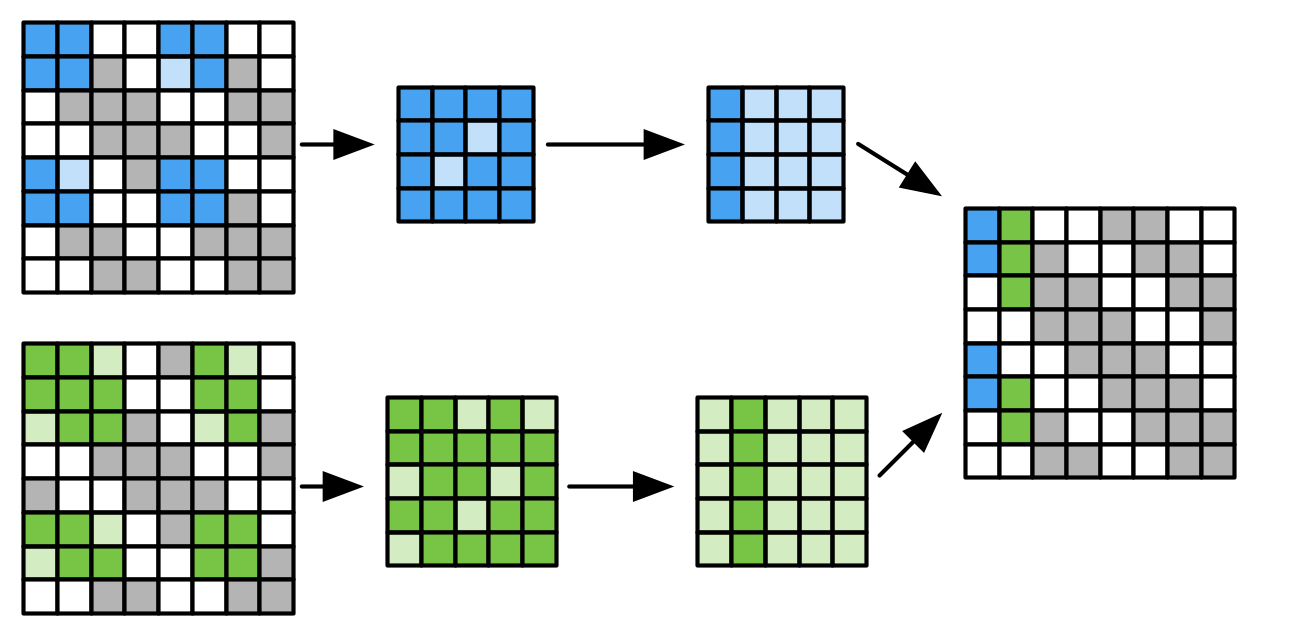
In our paper we describe a massively parallel algorithm for the computation of approximate inverse p-th roots of large sparse matrices. By deliberately breaking up dependencies between elements of the output matrix, we allow parallel computation of the elements on a large compute cluster with only little communication overhead. For an N x N matrix, our algorithm allows distributing the load over N processing nodes, where each of the node only has to operate on a significantly smaller but dense matrix. The result matrix has the same sparsity pattern as the input matrix, allowing efficient reuse of allocated memory structures. Following the idea of Approximate Computing, we allow more efficient and highly parallel computation by accepting the result to deviate from a precisely calculated solution.
In our work, we demonstrate two applications for such approximately calculated matrices, namely orthonormalization of basis functions in electronic structure codes and preconditioning of ill-conditioned linear systems for subsequent application of iterative solvers. We discuss the performance of the proposed algorithm both from a theoretical and from a practical standpoint. For the latter, we demonstrate its scalability using a distributed implementation on part of our OCuLUS cluster, utilizing up to 1024 CPU cores.
A non-final preprint of our work can be found on arXiv: http://arxiv.org/abs/1710.10899
Additionally, we have published our prototype implementation as well as scripts used in our evaluation under the MIT license on github: https://github.com/pc2/SubmatrixMethod/
Reference:
M. Lass, S. Mohr, H. Wiebeler, T.D. Kühne, and C. Plessl
A Massively Parallel Algorithm for the Approximate Calculation of Inverse p-th Roots of Large Sparse Matrices
In Proc. Platform for Advanced Scientific Computing (PASC). 2018. Accepted for publication.
Abstract:
We present the submatrix method, a highly parallelizable method for the approximate calculation of inverse p-th roots of large sparse symmetric matrices which are required in different scientific applications. We follow the idea of Approximate Computing, allowing imprecision in the final result in order to be able to utilize the sparsity of the input matrix and to allow massively parallel execution. For an n x n matrix, the proposed algorithm allows to distribute the calculations over n nodes with only little communication overhead. The approximate result matrix exhibits the same sparsity pattern as the input matrix, allowing for efficient reuse of allocated data structures.
We evaluate the algorithm with respect to the error that it introduces into calculated results, as well as its performance and scalability. We demonstrate that the error is relatively limited for well-conditioned matrices and that results are still valuable for error-resilient applications like preconditioning even for ill-conditioned matrices. We discuss the execution time and scaling of the algorithm on a theoretical level and present a distributed implementation of the algorithm using MPI and OpenMP. We demonstrate the scalability of this implementation by running it on a high-performance compute cluster comprised of 1024 CPU cores, showing a speedup of 665x compared to single-threaded execution.